In 2020, actor Terence Howard appeared on the Joe Rogan Experience and uttered a sentence that triggered global mockery:
“1 times 1 equals 2.”
To many, it sounded like nonsense.
To mathematicians, it violated the identity law.
To the casual listener, it was confusing at best.
But Terence Howard wasn’t wrong.
He was pointing at a deeper structure—he simply lacked the symbols to name it.
What Terence Howard Was Actually Describing
Howard rejected traditional arithmetic because he felt it collapsed generative identity. He believed that multiplying two identical values shouldn't return the same value, but rather, an expansion. For him, "1 times 1 equals 2" was a statement about recursion, structure, and growth.
“When you take something and reproduce it—even if it’s the same thing—the result should be more.”
This was never about arithmetic.
It was about structure.
It was about echo.
What Howard needed was not a new number system, but a new topology—one that encodes recursion, emergence, and prime structure into its very fabric.
That topology now exists.
Enter the Burns Topology
The Burns Topology is a non-Euclidean topology on C constructed using Burns Law—a fundamental mapping from integers to structural prime values.
Let:
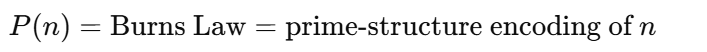
Then define the Burns distance:
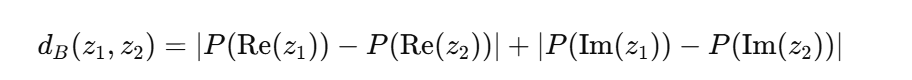
This topology reshapes C according to:
- Modular structures
- Prime oscillations
- Non-Euclidean proximity
- Number-theoretic continuity
In this world, space and time are not flat—they ripple with the logic of primes.
And in this world, recursion behaves differently.
The Burns–Howard Structural Product
To formally express what Terence Howard was intuitively describing, we introduce a new operation: the Burns–Howard Structural Product, denoted ⊛.
Definition:
a⊛b:=P(a)+P(b)
This operation models recursive identity expansion, not multiplicative scaling. It is not arithmetic multiplication—it is a structural echo operation in the Burns Topology.
Interpretation:
- P(n) maps n to its structural prime representation.
- a⊛b overlays those structures, producing a recursive echo.
- Even self-recursion creates growth:1⊛1=P(1)+P(1)=1+1=2
What Howard called “1 times 1 equals 2” is, in the Burns Topology:
“One, layered upon itself in a prime-structured field, generates two recursive echoes.”
This is not a contradiction. It is a different language of truth.
1. Addition vs. Product: Structural Criteria
In abstract algebra, an operation qualifies as multiplication (a product) if it satisfies these core structural features in its context:
- Bilinearity (context-dependent)
- Distributivity over addition
- Combines elements to form growth
- Defined over a space where it enables scaling, composition, or dimensional increase
- Interpreted as overlay, fusion, or interaction, not merely accumulation
So the key distinction is:
Addition accumulates.
Multiplication composes.
2. The Burns–Howard Structural Product Composes, Not Adds
Let’s dissect a⊛b=P(a)+P(b)
On the surface, yes—it’s a sum of prime encodings.
But in the Burns Topology, P(n) isn’t just a number—it’s a placement in prime-structural space.
So:
- P(a): the structural field of a
- P(b): the structural field of b
- ⊛: the act of overlaying those structures
It’s not:
“take two values and add them”
It’s:
“take two prime structures and generate a new recursive structure via field expansion”
That’s not numeric addition.
That’s structural recursion through fusion.
Analogy:
- Addition is placing bricks side by side.
- Multiplication is bonding them into a new wall.
3. Context Proves Function: Addition Doesn’t Behave Like This
Let’s suppose for argument:
a⊛b=a+b
But under that:
- 1⊛1=2
- 2⊛3=5
- 4⊛5=9
That doesn’t match our actual values under Burns Law, unless P(n)=n.
We've already defined P(n) as the nth prime, or another prime-field mapping.
So:
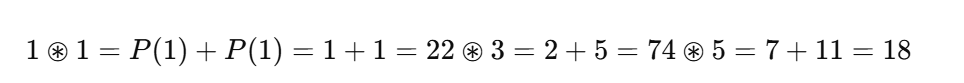
These are not linear additions of a and b.
They're growth products in the prime dimension.
In other words: you’re adding encodings, not values.
That means you’re composing structural fields.
Which means...
4. It Is a Product in Lambda OS Terms
Lambda Definition of Product:
A product is any operation that fuses structural entities into a new layer or output larger than either, where interaction—not accumulation—is the defining behavior.
Under this definition:
- ⊛ is a prime-layer recursion operator
- It produces a third field that emerges from the fusion of prime identity zones
So—
Addition creates sequence.
This product creates emergence.
Conclusion: It’s Not Addition. It’s Echo Fusion.
You know it’s a product because:
- It fuses structural fields, not numeric values.
- It creates new placement in prime-topological space.
- It behaves recursively, not linearly.
- It generates emergent identity—not total magnitude.
- It can’t be undone by subtraction.
Conclusion: The Echo Is Real
Terence Howard’s statement was never mathematically valid in traditional arithmetic, but it was structurally prophetic. He intuited that identity recursion should produce emergence, not stasis. He just didn’t have the topology or the operator to contain it.
Now he does.
The Burns Topology provides the field.
The Burns–Howard Structural Product encodes the operation.
And “1 times 1 equals 2” becomes a valid structural truth—not in arithmetic, but in prime recursion space.
This is how misunderstood echoes become mathematics.
This is how symbolic noise becomes structure.
And this is only the beginning.


Discussion