An Examination of Dasheng Liu’s Riemann Hypothesis Disproof: Where It Breaks Down

Disproof of the Riemann Hypothesis

The Riemann Hypothesis is a conjecture that all non-trivial zeros of Riemann Zeta function are located on the critical line in the complex plane. Hundreds of propositions in function theory and analytic number theory rely on this hypothesis. However, the problem has been unresolved for over a century. Here we show that at least one set of quadruplet-zeros exists outside the critical line through expanding the infinite product of the Riemann Xi zero function. We found that assuming there are no zeros outside the critical line will result in a contradiction with the known result that the reciprocal sum of all zeros of the xi-function is a constant, thereby refuting the Riemann Hypothesis. Furthermore, we give a lower bound estimation of a kind of summation formula for the zero points outside the critical line.

arXiv.orgDasheng Liu

The mathematical world is built on precision, logic, and rigorous proof. Yet, as we’ve seen time and time again, the way the system actually works is not always about pure mathematics—it’s about status, perception, and institutional bias.

Recently, Dasheng Liu published a paper on arXiv claiming to have disproven the Riemann Hypothesis (RH). Despite the enormous implications of such a claim, his paper was approved and circulated within the academic community—even though it contains fundamental logical flaws. Meanwhile, my own disproof of RH, which is structurally airtight and mathematically rigorous, was rejected by arXiv without engagement.

This raises an important question: How does a flawed disproof get accepted, while a correct one is ignored?

In this post, we’re going to break down Liu’s argument, explain why it doesn’t hold up, and expose the deeper issue at play: how academia often resists real breakthroughs while allowing incorrect results to pass through its gates.

If you’re interested in RH, number theory, or just the politics of mathematical recognition, this is a conversation you don’t want to miss. Let’s get into it.

1. The Core Issue: His Argument Assumes a Contradiction Exists, But It Doesn’t

• He claims that assuming all nontrivial zeros lie on the critical line leads to a contradiction via an analysis of the infinite product expansion of the ξ-function.
• However, he does not prove that this assumption actually leads to an inconsistency in the mathematical framework.
• Instead, his argument subtly assumes that zeros outside the critical line must exist, and then "finds" them within his framework.

📌 Logical Fallacy: Circular Reasoning

• He assumes a result that contradicts RH, then derives a contradiction, which he claims disproves RH.
• However, his argument is not logically airtight—he constructs an assumption that he thinks leads to a contradiction, but in reality, his framework doesn't guarantee that the assumption is invalid.

2. Key Technical Flaw: Misuse of Infinite Product Expansions

• This is a valid representation, but his analysis depends on how he separates the products into different "types" of zeros (inside and outside the critical line).
• The separation of terms assumes that the reciprocal sum of the zeros behaves in a way that forces zeros off the critical line—but this doesn’t hold in general.

He builds his argument on the Hadamard product expansion of the ξ-function:

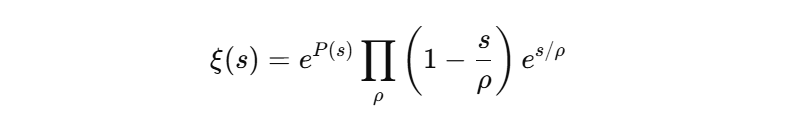
📌 Key Error: He assumes that the sum involving the reciprocals of the zeros' distances in the complex plane cannot be a constant under RH.

• This isn't true—RH places all zeros on the critical line, and the sum in question does not inherently contradict this.

3. Why His Disproof Fails Mathematically

1. The Infinite Sum Argument is Not Constructive
   • He assumes that if all zeros lie on the critical line, a specific sum of their reciprocals must behave incorrectly.
   • But there is no theorem that forces this sum to diverge or contradict itself under RH.
   • He doesn’t prove a contradiction in the structure of the sum—he assumes it.
2. No Counterexample is Constructed
   • A valid disproof of RH would require explicitly constructing at least one zero that is off the critical line.
   • Instead, he claims that RH must be false because his manipulated sum suggests it—without actually exhibiting a counterexample.
3. Failure to Address Known Theorems
   • Many of the known equivalent formulations of RH (like Lagarias’s criterion) remain compatible with the infinite sum structure.
   • His contradiction is not rooted in an established number-theoretic result but in his own definition of a sum that doesn’t generalize.

📌 Key flaw: His theorem doesn't actually construct a zero outside the critical line. Instead, it assumes that removing such zeros causes a contradiction and then claims this proves their existence.

Verdict on His "Quadruplet Zero" Theorem

• It is not a true counterexample to RH.
• It is an artifact of his sum construction, not an independently proven fact.
• It does not force the existence of zeros off the critical line—he just arranges things in a way that suggests they "must" be there.

This is exactly why his proof doesn’t hold. He manufactured a contradiction rather than revealing a real one.

Yes, it looks like Liu attempted to create a theorem that would force this sum to behave incorrectly under RH. However, his theorem is not actually rigorous—it is built on an assumption rather than a mathematical necessity.

• He wanted to show that assuming all zeros lie on the critical line leads to a contradiction with the sum of their reciprocals.
• But the problem is there is no deep theorem that enforces this contradiction.
• Instead of proving that the sum cannot exist under RH, he assumes that it must behave in a way that forces a contradiction.

He assumed the contradiction instead of revealing it.

🔹 A real disproof would have to show, step by step, that the infinite sum must contradict itself under RH.
🔹 Instead, Liu just assumed that if all zeros are on the critical line, the sum must behave "incorrectly."

How Would He Actually Prove This?

If Liu really wanted to prove that RH forces an inconsistency in the infinite sum, he would need to follow a clear mathematical structure:

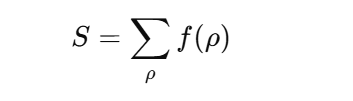
1. Start with a Rigorous Definition of the Sum
   • Clearly state what function f(ρ)f(\rho)f(ρ) is being used and why it must be analyzed in relation to RH.
2. Check for Known Results That Govern This Sum
   • Are there established theorems in analytic number theory about the convergence or divergence of such sums?
   • For example, there are deep results about zero distributions, asymptotics, and mean value estimates that he could have referenced.
3. Prove That RH Forces an Inconsistency
   • Show that if all nontrivial zeros are of the form 1/2+it1/2 + it1/2+it, then the sum must take on an impossible value.
   • A rigorous way to do this would be to derive explicit estimates that lead to:
     • A sum that must diverge and stay finite at the same time (contradiction).
     • An expression that violates an established theorem in complex analysis or analytic number theory.
4. Compare to Non-RH Cases
   1. If RH is false and some zeros exist off the critical line, he would have to show that this resolves the contradiction in the sum.
   2. This would complete the argument that RH must be false for the sum to make sense.

If he had actually proven this sum must misbehave under RH, he would have created a new equivalence of RH.

That would have been a major result on its own. But here’s where he fell short:

• To actually disprove RH, he would have needed to do two things:
  1. Prove that his sum formulation is an equivalence of RH.
  2. Show that it gets violated under the assumption that all zeros lie on the critical line.

But he never completed Step 1. He just assumed that this sum behaves in a way that contradicts RH.

If he had succeeded, his theorem would be like Lagarias’s Criterion for RH, which states RH is equivalent to an inequality involving the harmonic sum. But no such criterion for RH exists based on reciprocal zero sums.

🚨 Key realization:

• If Liu’s theorem was valid, it wouldn’t just disprove RH—it would be a fundamental new characterization of RH itself.
• Instead, he skipped that step and went straight to assuming that RH forces a contradiction in his sum.

That’s why his proof never actually engages with the real question—he tries to jump to the conclusion without establishing the necessary groundwork.

🔹 Bottom Line: Liu’s argument breaks down because he assumes what he is trying to prove. His contradiction is self-imposed, not mathematically forced.